Spice Modelling And Distortion Reduction

Analog Tape Recording

Kevin Aylward

kevin@kevinaylward.co.uk

Abstract

To reduce the distortion of analog magnetic tape records, a larger higher frequency, oscillator bias is added to the audio signal that is being recorded. The reason for this is to minimize the distortion that is generated due to the hysteresis of the magnetic material of the recording tape.

This article provides a technique for the construction of standard spice models that are able to model the essential characteristics of systems with this hysteresis. The technique allows for an approximation of sufficiently accuracy to illustrate hysteretic generated distortion and how it is reduced by the addition of high frequency bias.

In particular, the addition of a high frequency bias signal reduces distortion because the large positive and negative magnetizations of the core due to the oscillator bias signal, results in the audio signal magnetization being effectively a linear average of the oscillator bias signal.

Key words: high frequency bias, distortion, hysteresis, analog, tape recording, spice, modelling

A Hysteresis Model

The essential problem of modelling hysteresis is that it is a static or DC effect that has memory. That is, the next value depends not only on the present value, but also on the last value. However, this last value dependence does not depend on time. This results in a multivalued transfer function. Unfortunately, standard spice does not directly support this type of modelling. All dependence on the last value in spice is usually the result of a linear integration, which inherently results in frequency dependent transfer function and no account of distortion mechanisms. A way around this problem is to simply recognize that one can cheat. Analog models only have to do what they need to do, approximately, over a finite range of frequencies. Analysis shows that a small capacitor in conjunction with nonlinear diode resistances can be used to continuously store the last value of a signal before it changes slope direction to provide an effective hysteresis, but without unduly being dependent on frequency. This is in contrast to some spice “hysteresis” models that are only two output state models that do not allow for a continuous transfer function.

The Linear Model

The following schematic forms the basis of a continuous hysteresis model that may be used for modeling, for example, magnetic cores:

The output voltage of this block, essentially, linearly follows the input, but with an offset voltage. When the input turns around, the capacitor holds the voltage such that there is a dead band starting from the peak voltage reached. The key principle of operation is that there is nonlinear impedance that has a sharp ratio of resistances for forward and reverse bias conditions. The standard diode equation is the simplest, but not a necessary equation for the technique. It is used here to illustrate the method. Alternative equations may be used to fine tune the response characteristics. The input voltage may also be further processed in order to achieve different nonlinear transfer curves. The example here uses a behavioral model for the diodes of:

b1 a c i={is}*(exp({k}*v(a,c)) - 1)

To achieve an accurate model, the values of the components, are chosen such that frequency effects are minimized, over the range of frequencies that the system is desired to be modelled over. The time constant of Rload and Cmemory should be such that the last voltage before the turn around does not leak too much. The charging current through the drive impedance (diodes in this particular case) is such to not limit the response of the system over the desired operating frequency range.

The above topology results in the following set of transfer functions, and hysteresis graphs for various input voltages and frequencies:

Figure 1 – Ramped Input Transfer Function - F=1KHz, VIN=2V, 4V, 6V, 8V, 10V

Figure 2 – Ramped Input Transfer Function - F=1MHz, VIN=2V, 4V, 6V, 8V, 10V

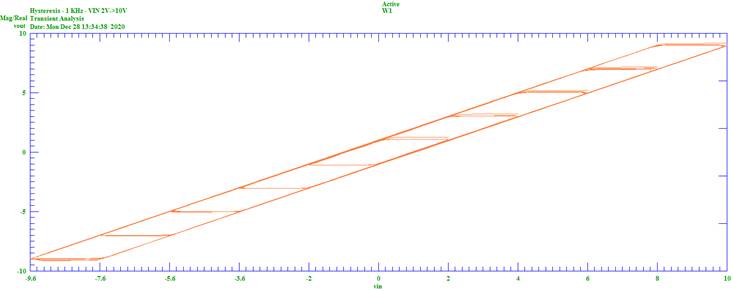
Figure 3 – Hysteresis - F=1kHz, VIN=2V, 4V, 6V, 8V, 10V

Figure 4 Hysteresis - F=1MHz, VIN=2V, 4V, 6V, 8V, 10V

The key points of the graphs, are that, over a 1000:1 frequency range, the voltage transfer function and the hysteresis voltage are relatively constant, thus forming a good approximation to real DC hysteresis.

In general, one constructs a spice behavioural resistance from a controlled current source that has the required forward and reverse characteristics. For example, the hysteresis dead band voltage may be adjusted by changing the diode parameter “N” from its default value of “1”.

Analog Tape Distortion

The above model can now be used to analysis distortion reduction in analog tape recorders when a high frequency sinewave bias signal is added to the analog signal to be recorded.

To first order, consider that the tape does not enter saturation such that this model does form a reasonable first order model to a real core. That is, the dead band reflects the remanence of the core and that this magnetic hysteresis results in a sinewave analog signal being clipped in a manner to that shown in figures 1 & 2, with hysteresis shown in figures 3 & 4. Thus, it is evident that these hysteresis characteristics, causes significant distortion.

Consider a large high frequency sinewave magnetization signal. Even with hysteresis, the average of the recorded signal will be zero. If this signal is now dc offset with another signal, the HF signals will now, essentially, swing around this offset signal, independent of the dead band as the large signal always drives the magnetization through the dead band. This is true, despite the HF signal having waveform distortion. Thus, the average of the HF bias signal will equal the offset signal, and it is this average value that forms the recorded signal for playback. In this way, the offset signal does not experience the dead band distortion as it would do if it was the only applied signal. The wave shape of the HF bias does not matter so long as its frequency is high enough such that all spurious signals are outside the bandwidth of the desired signal, as they can be filtered out. A schematic illustrating this is shown:

Figure 5 - Tape Distortion Reduction Schematic

The schematic shows the sum of 3 sinewave voltages. Two signals represent a multi frequency input, with the other, the HF bias signal. The two signals illustrate the effect of intermodulation distortion. A nonlinear system will show sum and difference frequencies.

Typical, raw single input/output signals are shown here:

Figure 6 - Single Frequency Signal, VIN=1V

Figure 7 - Single Frequency Signal, VIN=12V

Figure 6 & 7 shows the effective magnetization signal “voltage lagging” it’s input, and subsequently severely distorted due to the hysteresis that occurs when the signal changes direction. A standard spice technique that generates a voltage lag would not model this distortion of the waveform peaks.

The mixed, raw signal is shown here:

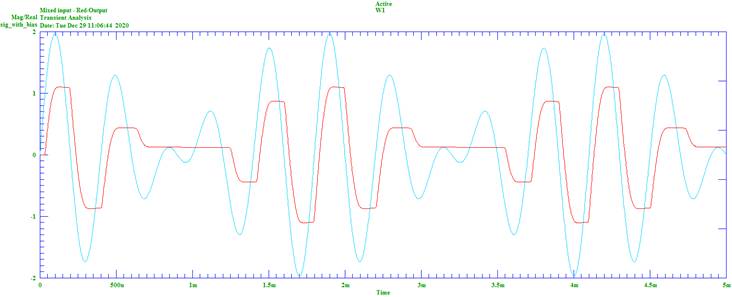
Figure 8 Mixed Frequency Signal, VINA=1V, VINB=1V

Figure 8 shows that there is significant distortion of the input signal.

FFTs of the mixed, unbiased signal are shown here:

Figure 9 - Unbiased Mixed Signal FFT VINA=1V, VINB=1V

Figure 10 Unbiased Mixed Signal FFT, VINA=6V, VINB=6V

These shows significant 500 Hz, 1kHz and 1k5 intermodulation distortion for the unbiased condition

The mixed, HF biased signal is shown here:

Figure 11 - HF Biased, Mixed Signal

The FFT of the mixed, HF biased signal is shown here:

Figure 12 - HF Biased Mixed Signal FFT

The addition of the HF bias thus shows greatly reduced intermodulation products.

Summary

This article has demonstrated a technique that allows for the modelling of hysteresis within the capabilities of standard Spice. It has also been shown how adding a high frequency bias signal to an audio signal reduces distortion.