Delta-Sigma ADC

Analog Design

Kevin Aylward B.Sc.

Delta-Sigma ADC

Alternative Linear Model

Overview

The purpose of this paper is to provide an explanation and understanding as to the basic theory of Delta-Sigma A/D converters. In particular, an alternative duty cycle linear/small signal model is proposed that is mathematically and physically consistent, in contrast to the standard linear model that is known to fail. It is not complete in the sense that it is assumed that the reader has already read some of the conventional literature on Sigma-Delta converters.

Essentially, all publications over the last 30 years or so describing the basics of Delta-Sigma adc noise shaping operation are incorrect.

By and large, these publications claim that the large amplitude gain at low frequencies result in the reduction of distortion of the 1 bit A/D in much the same manner as would be the case for conventional slightly non-linear feedback system. For example, the article:

“Delta-Sigma Modulators: Tutorial Overview, Design Guide, and State-of-the-Art Survey Circuits and Systems I:” IEEE Transactions on (Volume:58 , Issue: 1 ) pub Dec. 2010 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ J.M. de la Rosa

states:

“…Let us consider that the gain of the loop filter is large inside the signal band and small outside it. Due to the action of the feedback, the input signal, x, and the analog version of the modulator output, y, will practically coincide within the signal band. Consequently, most of the difference between both signals will be placed at higher frequencies, i.e., the quantisation error, eq, is shaped and most of its power is pushed outside the signal band…”

Technically, this statement is correct, however, the statement is referring to signal amplitudes, and is strictly false based on that assumption. The paper continues:

“Assuming that the quantiser in Fig. 6 is represented by the linear additive white noise model…”

This assumption is false, and such an assumption immediately leads to an incorrect physical conclusion.

Elementary feedback theory invalidates such a linear model for such a grossly non-linear system. It is a trivial aspect of analog amplifier theory that amplitude feedback can not reduce amplitude distortion of a limiting amplifier. This is proven in this paper, and illustrated in that such an assumption inherently results in noise shaping equations that disagree with experiment. Principally, because some of the comparator gain can theoretically and simply be moved to the integrator gain, whence, this incorrect model then implies distortion is modifiable by changing integrator gain, contrary to the known facts.

Additional facets of this, essentially, incorrect understanding of Delta-Sigma operation has, apparently, led to misunderstanding by some, of a fundamental error property of the Delta-Sigma converter that is a trivial consequence of acknowledging that the Delta-Sigma converter is a duty cycle modulator. This is the, apparently, previously unexplained (ref 4), property that noise tones with a frequency proportional to the average dc input up to mid scale, then folded, are produced. That is, this is what a Delta-Sigma ADC does by inherent design!

Introduction

Conventional descriptions of Delta-Sigma converters typically begin with a simplified block diagram of the physical schematic of a 1 Bit A/D Delta-Sigma converter. A particular linear model is then proposed with which it is alleged to mathematically show that quantisation “noise” is reduced by action of frequency gain processing in a feedback loop. The loop in this model is, essentially, based on instantaneous signal amplitudes such as voltage and current, although performed in the Laplace S, or discrete time Z domains.

A basic problem with this approach is that the only rational interpretation of a reasonable formulation for such a model is that the model predicts that the noise should be reducible to zero, for all frequencies, despite the universal consensuses in the community is that the model correctly predicts “noise shaping” with a result that apparently agrees with the detailed non-linear time simulations and physical results. In order to achieve this result the universal consensus also unilaterally agree to set an inherent integrator gain constant parameter of the model to unity, despite there being no mathematical or physical basis to make such an assumption, and that detailed simulations show that the noise is independent of such gain constant, even by several orders of magnitude change. What is perhaps even more note worthy is that this basic anomalous result of the integrator gain constant is also fully known in the community, yet the notion that this anomaly actually means that the purported explanation of noise filtering by the feedback loop is therefore false, appears to go unnoticed. Many papers reiterate that the linear model, as proposed, explains noise filtering when clearly, cherry picking the one specific value of a parameter so that it fits a desired result is no explanation at all, and that an alternative approach is required. Indeed, accepting such an explanation may be said to be on a par of using the Phlogiston theory of fire to explain a one off occurrence of burning.

It is shown here that the root cause of the failure of the standard linear model is due to the following:

1 Failure to recognise the basic incorrectness of applying linear voltage/current theory to a 1 Bit A/D converter.

2 Failure to recognise that the Delta-Sigma converter is not an over-sampled PCM converter but, essentially, it is inherently a (variable discrete ) duty cycle modulator (strictly, a pulse density modulator). That is, the Delta-Sigma converter achieves its accuracy by converting signals in the amplitude (voltage/current) domain to the time domain. Measurements in the time domain are then converted back to the amplitude domain.

The distinction between PCM and (effective) PWM has a drastic effect on anticipated distortion. This can be ascertained from comparing to the non quantised equivalents, linear PAM (pulse amplitude modulation) and linear PWM. For the PAM signal, only frequencies at NF_s +/- F_m are produced. For PWM a spectrum of NF_s +/- MF_m are produced.

Standard Delta-Sigma Physical Model

A standard block diagram of the Delta Sigma operation blocks is shown:

Fig. 1

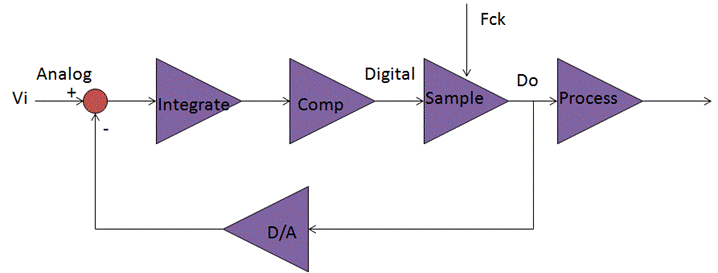
The basic operation being described as:

The difference between the input voltage and output voltage is integrated in a direction such that if the input is not equal to the digital output, converted to analog, the digital output will, after time, be switched to an output value that will attempt it to equal the input. The net result is that the average of the digital switching output will be forced to equal the average input scaled by the DAC reference voltage.

The average of the digital output is given by the ratio of the number digital highs to the sum of high and lows. These numbers are determined by counts in time, determined by a reference clock, and so the average may have a resolution determined by as many counts are counted. Thus, the Sigma-Delta converter converts an input voltage to time, and this time is then converted to a digital representation of the inputs amplitude.

Specifically, the integrator capacitor cannot pass a steady state DC current, as it is an open circuit for DC. That is, a capacitor’s average current must be exactly zero. This is so, even if the capacitor is non-linear. For a typical converter with a common summing junction for the input and feedback signals, this means that the average of the feedback current minus the input current must be zero.

It is noted that the distinction between a standard multibit PCM is that a for PCM a single sample represents, essentially, a valid representation of the input signal. For a Delta-Sigma converter, a single sample represents, essentially, nothing. Only multiple samples, have any meaning in such a converter. This distinction is of fundamental importance when attempting to form a linearised model of the Delta-Sigma converter.

Nominal Characteristics

The acknowledgment that the Delta-Sigma converter is fundamentally and inherently a (variable) duty cycle based converter, and not a PCM converter, allows a number of points to be made.

The actual average duty cycle does not usually dictate a unique switching frequency. However, any repetitive average duty cycle due to a constant DC voltage well result in a “noise” or idle tone frequency component. That is:

τ T = V i V r MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacqaHepaDaeaacaWGubaaaiabg2da9maalaaabaGaamOvamaaBaaaleaacaWGPbaabeaaaOqaaiaadAfadaWgaaWcbaGaamOCaaqabaaaaaaa@3DA6@

For a system nominally referenced to a 0V to V_ref DAC output voltage.

The period T, and hence the idle tones, may well change with time as the system hunts to obtain a duty cycle that equals the relative input voltage, however the minimum frequency is dictated by the sampling frequency in that τ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiXdqhaaa@37AA@ can not be less than the sampling period. Therefore, a Delta-Sigma converter may well have at least one error frequency no higher than:

F min = V i V r F s MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOramaaBaaaleaaciGGTbGaaiyAaiaac6gaaeqaaOGaeyypa0ZaaSaaaeaacaWGwbWaaSbaaSqaaiaadMgaaeqaaaGcbaGaamOvamaaBaaaleaacaWGYbaabeaaaaGccaWGgbWaaSbaaSqaaiaadohaaeqaaaaa@40C4@

This minimum frequency duty cycle will set a limit to the minimum dc quantisable signal at Fs for a 1 bit converter as follows.

The output can only switch from n 0s to one 1 pulse at an on time of 1/Fs.

The minimum duty cycle possible is therefore D min = τ o n τ o MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaBaaaleaaciGGTbGaaiyAaiaac6gaaeqaaOGaeyypa0ZaaSaaaeaacqaHepaDdaWgaaWcbaGaam4BaaqabaaakeaacaWGUbGaeqiXdq3aaSbaaSqaaiaad+gaaeqaaaaaaaa@4193@

This represents an output frequency of F o_min = 1 n τ o = F s n MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOramaaBaaaleaacaWGVbGaai4xaiGac2gacaGGPbGaaiOBaaqabaGccqGH9aqpdaWcaaqaaiaaigdaaeaacaWGUbGaeqiXdq3aaSbaaSqaaiaad+gaaeqaaaaakiabg2da9maalaaabaGaamOramaaBaaaleaacaWGZbaabeaaaOqaaiaad6gaaaaaaa@4544@ and an average dc output voltage of V min = V ref n MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaaBaaaleaaciGGTbGaaiyAaiaac6gaaeqaaOGaeyypa0ZaaSaaaeaacaWGwbWaaSbaaSqaaiaadkhacaWGLbGaamOzaaqabaaakeaacaWGUbaaaaaa@3FAE@ .

This is an inherent lower limit for determining a V_min input, as is not possible to achieve a smaller duty cycle than that which is dictated by n.

To enable this frequency to be filtered out, the input frequency must therefore satisfy:

F s > V i V ref F i =n F i MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOramaaBaaaleaacaWGZbaabeaakiabg6da+maalaaabaGaamOvamaaBaaaleaacaWGPbaabeaaaOqaaiaadAfadaWgaaWcbaGaamOCaiaadwgacaWGMbaabeaaaaGccaWGgbWaaSbaaSqaaiaadMgaaeqaaOGaeyypa0JaamOBaiaadAeadaWgaaWcbaGaamyAaaqabaaaaa@449F@

That is, if n is made larger to achieve a lower coded input voltage, then the input frequency must be reduced so that the minimum frequency duty cycle frequency can be filtered out.

Note that the argument is flipped when considering the maximum duty cycle. In this case n represents voltages reducing away from the maximum, which reduces the frequency. Essentially, predictions for F_min > Fs/2 are folded down to a lower frequency about Fs/2.

This means that to achieve a true resolution of 1/n, the signal must be over sampled by n in a 1 bit Delta Sigma converter. This is so, irrespective of the order of the modulator, despite contrary statements in the literature, although this has been recognised in the literature (ref 12). Any attempt to produce the exact same average duty cycle can only result in lower frequency components as it is not possible to have smaller on or off times than that dictated by the clock period.

This has been verified in simulations. A typical semi ideal simulation in the SuperSpice simulator produced the following waveforms for a full scale of 0V to 5V set to nominally 1/100, or 50mv, of full scale DC input with a clock of 1Mhz, The output frequency was measured at 10.05kHz, with the average digital output measured at 50.00mV. Also confirmed were inverted waveforms for 50mV away from full saclae i.e 4.95V for these simulations.

Fig. 2

100^th full scale Delta-Sigma digital output and 16 kHz filtered DC voltage output

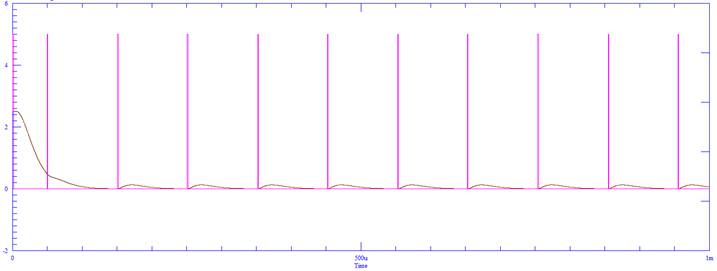
It may be noted, that in general, mid range voltages typically allow for the duty cycle to oscillate, pseudo randomly, such that the duty cycle may go high and low but still achieve a net average 0 and 1’s density that corresponds to an exact V_in/V_ref but which has no fundamental steady state oscillation error noise frequency. However, any rational value of V_in/V_ref will result in an exact solution to the ideal feedback property of the system that τ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiXdqhaaa@37AA@ /T = V_in/V_ref, therefore at such rational values, tones should be generated.

Standard Delta-Sigma Linear Noise Model

A standard block diagram of the Delta Sigma linear noise model is shown:

Fig. 3

The physical 1 Bit A/D (comparator) has been replaced by a unity gain summer with an added error source representing the error between the A/D output and its analog input. The input and output voltages have been replaced by a Z domain representation of the instantaneous signal amplitudes. However, although it is often noted that such a gross linearisation approximation to the A/D has some issues, its true nature that such a model is, essentially, useless, is usually ignored. Possibly because the end justifies the means!

It is now shown that such a model in a transfer function feedback loop is fundamentally invalid, and that such a model inherently results in a model with predictions that disagree with reality.

Invalidity Of The 1 Bit A/D Noise Model

Consider an amplifier driving a 1 bit A/D converter. It is shown here that such a system is so grossly non linear that voltage/current transfer feedback can not reduce the distortion as would be the case for relatively weakly non linear systems. This is actually, intuitively obvious, for clearly if the output of a block can only be one of two values by design, nothing can be done to change those values. It is however instructive to formally show this by general feedback theory, as for example in the paper Feedback Distortion, from which a key argument is repeated here, and should be read to gain an understanding as to when feedback is able to reduce distortion..

Fig. 4

V_o is either V_r or – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ V_r depending on whether A.V_d is greater or less than zero.

It is sometimes proposed to model such a system by the following:

Fig. 5

For the non feedback case, an expression for the output V_o is assumed to be of the form:

V o =S+D MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAfadaWgaaWcbaGaam4BaaqabaGccqGH9aqpcaWGtbGaey4kaSIaamiraaaa@3BB8@

That is, the wanted signal, S, plus an error term D.

In which case, the relations for S and D would be, for Vi > 0₊:

S=A V i MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadofacqGH9aqpcaWGbbGaamOvamaaBaaaleaacaWGPbaabeaaaaa@3AC3@

D=(1− A V i V r ) V r MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaceaa4JIaamiraiabg2da9iaacIcacaaIXaGaeyOeI0YaaSaaaeaacaWGbbGaamOvamaaBaaaleaacaWGPbaabeaaaOqaaiaadAfadaWgaaWcbaGaamOCaaqabaaaaOGaaiykaiaadAfadaWgaaWcbaGaamOCaaqabaaaaa@42F8@

V o =A V i +(1− A V i V r ) V r MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAfadaWgaaWcbaGaam4BaaqabaGccqGH9aqpcaWGbbGaamOvamaaBaaaleaacaWGPbaabeaakiabgUcaRiaacIcacaaIXaGaeyOeI0YaaSaaaeaacaWGbbGaamOvamaaBaaaleaacaWGPbaabeaaaOqaaiaadAfadaWgaaWcbaGaamOCaaqabaaaaOGaaiykaiaadAfadaWgaaWcbaGaamOCaaqabaaaaa@46B8@

Because for any value V_i greater than zero, the output, V_o, is the constant V_r. A similar expression may be written for the case is less than zero. Applying feedback by letting V_i -> V_i - V_o:

V o =A( V i − V o )+(1− A( V i − V o ) V r ) V r MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAfadaWgaaWcbaGaam4BaaqabaGccqGH9aqpcaWGbbGaaiikaiaadAfadaWgaaWcbaGaamyAaaqabaGccqGHsislcaWGwbWaaSbaaSqaaiaad+gaaeqaaOGaaiykaiabgUcaRiaacIcacaaIXaGaeyOeI0YaaSaaaeaacaWGbbGaaiikaiaadAfadaWgaaWcbaGaamyAaaqabaGccqGHsislcaWGwbWaaSbaaSqaaiaad+gaaeqaaOGaaiykaaqaaiaadAfadaWgaaWcbaGaamOCaaqabaaaaOGaaiykaiaadAfadaWgaaWcbaGaamOCaaqabaaaaa@4F4D@

V o (1+A−A)=A V i +(1− A V i V r ) V r MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAfadaWgaaWcbaGaam4BaaqabaGccaGGOaGaaGymaiabgUcaRiaadgeacqGHsislcaWGbbGaaiykaiabg2da9iaadgeacaWGwbWaaSbaaSqaaiaadMgaaeqaaOGaey4kaSIaaiikaiaaigdacqGHsisldaWcaaqaaiaadgeacaWGwbWaaSbaaSqaaiaadMgaaeqaaaGcbaGaamOvamaaBaaaleaacaWGYbaabeaaaaGccaGGPaGaamOvamaaBaaaleaacaWGYbaabeaaaaa@4C26@

V o =A V i +(1− A V i V r ) V r MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAfadaWgaaWcbaGaam4BaaqabaGccqGH9aqpcaWGbbGaamOvamaaBaaaleaacaWGPbaabeaakiabgUcaRiaacIcacaaIXaGaeyOeI0YaaSaaaeaacaWGbbGaamOvamaaBaaaleaacaWGPbaabeaaaOqaaiaadAfadaWgaaWcbaGaamOCaaqabaaaaOGaaiykaiaadAfadaWgaaWcbaGaamOCaaqabaaaaa@46B7@

This expression is, as expected, clearly, the same as the original expression, therefore, for a 1 Bit A/D, voltage/current transfer function, feedback can do nothing to the inherent signal to distortion/error ratio. That is, standard linear feedback loop analysis for the 1 bit A/D converter, for essentially instantaneous voltage/current signals is completely invalid.

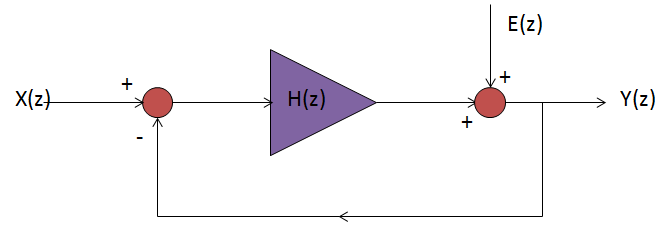
Standard Delta-Sigma Noise Analysis

A standard block diagram of Delta Sigma linear noise analysis is shown:

Fig. 6

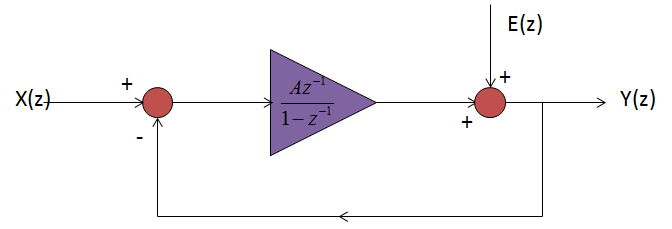
In standard treatments, the gain factor A is omitted, however there is no mathematical or physical justification for this omission. The main block represents the Delta Sigma integrator. This integrator feeds an A/D converter, that is, a comparator, which is ideally, an infinite gain amplifier. Some of the gain of the comparator can logically, simply be assigned to the integrator as the integrator and comparator are in series cascade. The analysis of the loop then results in:

Y(z)= X(z)A z −1 1+(A−1) z −1 + E(z)(1− z −1 ) 1+(A−1) z −1 MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMfacaGGOaGaamOEaiaacMcacqGH9aqpdaWcaaqaaiaadIfacaGGOaGaamOEaiaacMcacaWGbbGaamOEamaaCaaaleqabaGaeyOeI0IaaGymaaaaaOqaaiaaigdacqGHRaWkcaGGOaGaamyqaiabgkHiTiaaigdacaGGPaGaamOEamaaCaaaleqabaGaeyOeI0IaaGymaaaaaaGccqGHRaWkdaWcaaqaaiaadweacaGGOaGaamOEaiaacMcacaGGOaGaaGymaiabgkHiTiaadQhadaahaaWcbeqaaiabgkHiTiaaigdaaaGccaGGPaaabaGaaGymaiabgUcaRiaacIcacaWGbbGaeyOeI0IaaGymaiaacMcacaWG6bWaaWbaaSqabeaacqGHsislcaaIXaaaaaaaaaa@5BBB@

Where X(Z), Y(Z) are the Z transform of the instantaneous time domain amplitudes (voltages) x(KT), y(KT)

The standard treatment with A=1 simply gives:

Y(z)=X(z) z −1 +E(z)(1− z −1 ) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMfacaGGOaGaamOEaiaacMcacqGH9aqpcaWGybGaaiikaiaadQhacaGGPaGaamOEamaaCaaaleqabaGaeyOeI0IaaGymaaaakiabgUcaRiaadweacaGGOaGaamOEaiaacMcacaGGOaGaaGymaiabgkHiTiaadQhadaahaaWcbeqaaiabgkHiTiaaigdaaaGccaGGPaaaaa@4A5B@

Whence it is claimed that the noise is reduced for low z frequencies, i.e. z approaching unity, and that noise is increased as frequency increases thereby resulting in “noise shaping” of the initially huge 1 bit DAC error.

First – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbiqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C3@ The standard equation, based in the standard assumptions, is physically and mathematical gibberish.

Consider the case of a constant DC input voltage. In this case Z=1, whence the equation then implies that:

Y(z)=X(z) z −1 MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVDI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMfacaGGOaGaamOEaiaacMcacqGH9aqpcaWGybGaaiikaiaadQhacaGGPaGaamOEamaaCaaaleqabaGaeyOeI0IaaGymaaaaaaa@406E@ and hence y(kt) = x(kt_d-t_d), that is the output voltage is simple a delayed input voltage.

This is, of course false. If for example, the input x=0.635324 V the output can still only be – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ V_ref1 or +V_ref2.

It is only the average of the output voltage over a period of time that, in the limit, approaches the input voltage. The standard treatments confuse instantaneous amplitude concepts and time average concepts, and hence the equations are completely meaningless on that basis.

As yet it is not clear how to reformulate the equations so that they can make mathematically and physical sense. In principle, equations might be set-up in terms of the Z transforms of averages, rather than instantaneous values. Integrating the equation with respect to time and taking the limit for large time might then well show that the average error goes to zero so that the average output voltage equals the average input voltage. However, this is troublesome for say, a sine wave input as the average of a sine is zero. The integration period would have to be large enough to eliminate the distortion, but small enough to not filter out the signal.

Second - why chose A=1? The full expression shows that if A is made very large, then the noise term should be reducible to as low as desired.

It is known, for example reference 3, that full transient simulations, and practice, show that the noise is completely independent of the integrator gain constant A. This linear model is therefore proven to be false. It can only agree with reality by the single cherry picked assumption that A=1. The model therefore offers no explanation as to why A/D error noise is “shaped” and reduced for low frequencies, as the filter can not possibly be operating on amplitude information that is quenched by the comparator.

The reason for the failure of the model is simple.

A linear amplitude feedback model is not valid for a 1 Bit A/D feedback system.

A Delta-Sigma converter operates as a time converter, not as an amplitude converter.

Alternative Delta-Sigma Linear Model

A linear Delta-Sigma model should recognise that that the feedback signal from the A/D converter is, essentially, a duty cycle.

Consider the following two expressions:

V=( V p sin( ω i t)) τ Τ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvaiabg2da9iaacIcacaWGwbWaaSbaaSqaaiaadchaaeqaaOGaci4CaiaacMgacaGGUbGaaiikaiabeM8a3naaBaaaleaacaWGPbaabeaakiaadshacaGGPaGaaiykamaalaaabaGaeqiXdqhabaGaeuiPdqfaaaaa@469B@

V= V p ( τ Τ sin( ω i t)) MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvaiabg2da9iaadAfadaWgaaWcbaGaamiCaaqabaGccaGGOaWaaSaaaeaacqaHepaDaeaacqqHKoavaaGaci4CaiaacMgacaGGUbGaaiikaiabeM8a3naaBaaaleaacaWGPbaabeaakiaadshacaGGPaGaaiykaaaa@469B@

They are the same, but may be taken as representing as either a sine voltage signal with a gain constant τ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiXdqhaaa@37AA@ /T, or a sine duty cycle signal with a gain constant Vp. The result of passing this signal through a low pass filter is identical, whatever the interpretation of what the signal represents. This illustrates why distinguishing between treating a Delta-Sigma converter as an over sampled PCM converter rather than a time converter may be subject to confusion. A low pass filter also demodulates a duty cycle signal, such that it may be misinterpreted as an amplitude filtered signal.

The Basics of the Alternative Model

Consider an input voltage of effective ¼ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=Xlaaaa@384A@ full scale, with full scale being 5V, and chosen to produce convenient steady state waveforms, and a DC output demodulated output. A typical simulation of this condition results in the following waveforms:

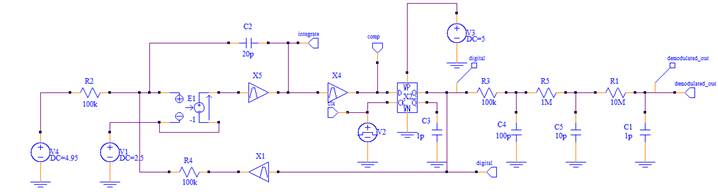
Fig. 7

The red trace being the sampling clock (negative edge triggered), the green wave being the integrator output, the violet being the digital output. The digital output is overlaid on to the clock and can be seen to occur at changes in slope direction. The operation is as follows:

When the digital output is low, the integrator ramps up in an effort to switch the digital output high. When it reaches the comparator (mid scale) threshold it switches the comparator that then attempts to instruct the integrator to start ramping down. In this example, it does this, essentially, immediately as the sample clock is aligned to this time point. This means that the comparator input is now such that it should turn back high again, as its input has now ramped down almost immediately below its switch point. However, this instruction is delayed by the D-Type until the next available sample clock edge. On that next edge the integrator starts ramping back up again. Thus, it can be seen that a constant steady state time waveforms is achieved for the ¼ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=Xlaaaa@384A@ full scale input of 1 clock pulse up for every 3 clock pulses down.

If the input was slightly different from ¼ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=Xlaaaa@384A@ full scale, it gets much more complicated. However, it can be seen that the down slope will either be short or be to long because the sample clock will not be able to switch at the exact duty cycle point that such a different input would require. There is thus an error in achievable duty cycle dictated by the sampling period. This is the root cause of quantisation error in the Delta-Sigma converter. The system will still attempt to force a τ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiXdqhaaa@37AA@ /T average duty cycle equal to the average input, but time quantisation means that, T will vary with time and manifest as an error source, ideally randomly, but in actuality with various frequencies. The peak magnitude of the quantisation “tau noise” is thus:

τ np = 1 F s MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiXdq3aaSbaaSqaaiaad6gacaWGWbaabeaakiabg2da9maalaaabaGaaGymaaqaaiaadAeadaWgaaWcbaGaam4Caaqabaaaaaaa@3D88@

In general, the actual time waveforms may get very complicated. The ¼ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=Xlaaaa@384A@ scale waveform produced a constant triangle wave from the comparator. For other inputs the “overshoot” due to the sampling clock delay produces other waveform types because both slopes continue until the clock allows the comparator state to be fed back to the integrator. A 1/10^th full scale input is shown here:

Fig. 8

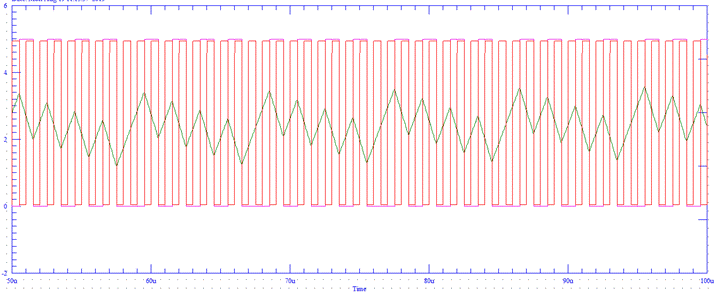
It is be noted that there is a duty cycle within a duty cycle. That is, the single cycle duty cycle oscillates within another approximate triangle wave duty cycle. Although the duty cycle oscillation, in this case is approximately triangular, arguably, it may be approximated to first order by a sine wave such that the “instantaneous” duty cycle may be expressed as:

D n =( τ T o )sin( ω n t) MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaBaaaleaacaWGUbaabeaakiabg2da9iaacIcadaWcaaqaaiabes8a0bqaaiaadsfadaWgaaWcbaGaam4BaaqabaaaaOGaaiykaiGacohacaGGPbGaaiOBaiaacIcacqaHjpWDdaWgaaWcbaGaamOBaaqabaGccaWG0bGaaiykaaaa@462E@

Where it is recognised that the sub duty cycle variations produces a lower frequency noise ripple frequency in the demodulated output.

Duty Cycle Noise

As noted, there is a noise error in the output duty cycle, due to time quantisation, given by a peak step size of:

By the usual statistical arguments, it may be stated that this time error can be expressed as a mean square error of:

σ τn = 1 12 F s MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaSbaaSqaaiabes8a0jaad6gaaeqaaOGaeyypa0ZaaSaaaeaacaaIXaaabaWaaOaaaeaacaaIXaGaaGOmaaWcbeaakiaadAeadaWgaaWcbaGaam4Caaqabaaaaaaa@3FF2@

The on time, which determines the average duty cycle, and hence the average converted voltage, is obtained by discrete additive counts of this 1/F_s step size as n/m. Assuming that the duty cycle is changing, essentially, statistically randomly as it hunts to the true average value, then the total error in the quantisation time will be given by a power sum such that:

σ τon = n σ τn MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaSbaaSqaaiabes8a0jaad+gacaWGUbaabeaakiabg2da9maakaaabaGaamOBaaWcbeaakiabeo8aZnaaBaaaleaacqaHepaDcaWGUbaabeaaaaa@424F@

Where the output duty cycle, proportional to V_in/V_ref, is expressed by:

D o = τ o T o = n τ s m τ s MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaBaaaleaacaWGVbaabeaakiabg2da9maalaaabaGaeqiXdq3aaSbaaSqaaiaad+gaaeqaaaGcbaGaamivamaaBaaaleaacaWGVbaabeaaaaGccqGH9aqpdaWcaaqaaiaad6gacqaHepaDdaWgaaWcbaGaam4CaaqabaaakeaacaWGTbGaeqiXdq3aaSbaaSqaaiaadohaaeqaaaaaaaa@46B6@

This results in a nominal duty cycle/voltage quantisation “noise” error as:

D nr = V nr = σ τon / T o τ o / T o = n σ τn n τ s = 1 n 12 MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaBaaaleaacaWGUbGaamOCaaqabaGccqGH9aqpcaWGwbWaaSbaaSqaaiaad6gacaWGYbaabeaakiabg2da9maalaaabaGaeq4Wdm3aaSbaaSqaaiabes8a0jaad+gacaWGUbaabeaakiaac+cacaWGubWaaSbaaSqaaiaad+gaaeqaaaGcbaGaeqiXdq3aaSbaaSqaaiaad+gaaeqaaOGaai4laiaadsfadaWgaaWcbaGaam4BaaqabaaaaOGaeyypa0ZaaSaaaeaadaGcaaqaaiaad6gaaSqabaGccqaHdpWCdaWgaaWcbaGaeqiXdqNaamOBaaqabaaakeaacaWGUbGaeqiXdq3aaSbaaSqaaiaadohaaeqaaaaakiabg2da9maalaaabaGaaGymaaqaamaakaaabaGaamOBaaWcbeaakmaakaaabaGaaGymaiaaikdaaSqabaaaaaaa@5B24@

This expression simply represents that, with a fixed time quantisation error, increasing the measurement time results in that time being known relatively more accurately.

Consider the cases where m=n+1, and n >>1, with n stepped. That is, duty cycles > 50%. This will produce a rectangular voltage error output with a steady state duty cycle, at a frequency:

F n = 1 2 τ s (n+1) ~ F s 2n MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOramaaBaaaleaacaWGUbaabeaakiabg2da9maalaaabaGaaGymaaqaaiaaikdacqaHepaDdaWgaaWcbaGaam4CaaqabaGccaGGOaGaamOBaiabgUcaRiaaigdacaGGPaaaaiaac6hadaWcaaqaaiaadAeadaWgaaWcbaGaam4CaaqabaaakeaacaaIYaGaamOBaaaaaaa@45FB@

Therefore, the D_nr can be expressed by substituting for n, as:

D nr = 1 12 . 1 F s 2 F n = D nr OSR MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaBaaaleaacaWGUbGaamOCaaqabaGccqGH9aqpdaWcaaqaaiaaigdaaeaadaGcaaqaaiaaigdacaaIYaaaleqaaaaakiaac6cadaWcaaqaaiaaigdaaeaadaGcaaqaamaalaaabaGaamOramaaBaaaleaacaWGZbaabeaaaOqaaiaaikdacaWGgbWaaSbaaSqaaiaad6gaaeqaaaaaaeqaaaaakiabg2da9maalaaabaGaamiramaaBaaaleaacaWGUbGaamOCaaqabaaakeaadaGcaaqaaiaad+eacaWGtbGaamOuaaWcbeaaaaaaaa@491D@

Where OSR is the so called Over Sampling Ratio. This is because if the input frequency is greater than this noise frequency, then this noise frequency cannot be filtered out. So, the input frequency must be chosen to be less then than this noise frequency, and in the limit, be equal to this noise frequency, so that the duty cycle noise can then be expressed as:

D nr = 1 12 . 1 F s 2 F i = D nr OSR MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaBaaaleaacaWGUbGaamOCaaqabaGccqGH9aqpdaWcaaqaaiaaigdaaeaadaGcaaqaaiaaigdacaaIYaaaleqaaaaakiaac6cadaWcaaqaaiaaigdaaeaadaGcaaqaamaalaaabaGaamOramaaBaaaleaacaWGZbaabeaaaOqaaiaaikdacaWGgbWaaSbaaSqaaiaadMgaaeqaaaaaaeqaaaaakiabg2da9maalaaabaGaamiramaaBaaaleaacaWGUbGaamOCaaqabaaakeaadaGcaaqaaiaad+eacaWGtbGaamOuaaWcbeaaaaaaaa@4918@

Comparator/Sampler Linear Duty Cycle Model

Unlike in the amplitude domain, an ideal comparator produces no error for a τ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiXdqhaaa@37AA@ /T input, and so a τ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiXdqhaaa@37AA@ /T model for the comparator and sampler may be constructed as follows:

Fig. 9

Fig. 6

The output of the comparator is simply the input duty cycle from the integrator added to a noise duty cycle signal due to the error caused by the sampling quantising the time.

Integrator Linear Duty Cycle Model

Fig. 3 shows that the integrator output zero crossings, i.e., what constitutes the integrator’s output duty cycle signal to the comparator, are simply a delayed version of the zero crossings of its input. Furthermore, these zero crossings are clearly independent of the integrator gain. Changing the physical integrator gain only changes the amplitude of the integrator triangle output, which the comparator does not care about as it only senses zero crossings. Qualitatively, the delay of the triangle zero crossings from its peak, dictated by its input, may be viewed as equivalent to the delay of a sine wave peak to its zero crossings, which is 90 degrees, such that for a duty cycle model, the integrator still behaves as an integrator for its input output transfer function. That is, as a 1/(1- z^-1) in the Z domain, and 1/s in the Laplace domain. Indeed, the equivalence of a demodulated output of a PWM signal, as expressed by the equivalence of:

Shows that any filter will process a PWM signal in essentially the same manner as that of an amplitude signal.

It is noted that in general, the zero crossings of the output of an integrator, do not usually remain the same as that of it input. For an open loop integrator, any average DC due to unequal duty cycle will result in an ever increasing amplitude output.

However, for the integrator, it still remains to determine its gain constant for an applied duty cycle transfer function. As the output duty cycle of the integrator is the same as its input duty cycle, the small signal transfer gain of the integrator model for a sinusoidal duty cycle variation must then also be unity.

Consider the following block continuous time model:

Fig. 7

An analysis of the above model, and confirmation simulations, shows that K must be 1 if the modulation frequency is to result in equal amplitude demodulated PWM outputs at that frequency. That is, equal effective PWM signals prior to the LPF, irrespective of the triangle and rectangular input waveform shapes to the LPFs. The duty cycle is changed at the rate of the sample frequency Fs, hence the constant K, should be set to 1 at Fs, which sets K to unity for the Z domain integrator.

Thus, the duty cycle, Z domain linear model for the Delta-Sigma converter is:

Fig. 10

Aylward Duty Cycle Model

Where it may be noted that there is now no room to move the comparator gain into the integrator gain as the comparator has been necessarily modelled by a unity gain duty cycle transfer function, not as an amplifier.

Time Domain View of Noise Shaping

A higher frequency, variable duty cycle is produced so that the average of the duty cycle still produces the same average of the input voltage ratio.

A search on the internet, despite there being many tutorials on Delta-Sigma converters, essentially, turns up nothing for any time domain explanations of so called “noise shaping”. Typically there is an overview and then a jaunt into the small signal (flawed) model, essentially, allegedly claiming that the amplitude “noise” of the comparator gets filtered in such a way as to “push low frequency noise up in frequency”. What is really happening?

For voltages near full scale or zero, and with 1/N ratio, it is has been illustrated that a constant τ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiXdqhaaa@37AA@ /T digital output at a sample frequency/N is produced. For ratios where there is room for higher and lower τ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVv0Je9sqqrpepC0xbbL8F4rqaqFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiXdqhaaa@37AA@ /T lower ratios, things are different. Consider a 269/1024 ratio, chosen specifically as a prime number numerator so that there is only one exact solution to the average voltage that that ratio represents, i.e. 0.26269. Simulations show that this does not produce an exact 269 count/1024 count at a 1024 times sample period, but what initially appears to be a 1 count/5 count, representing 0.2 at a much higher frequency, but still with the correct average output voltage! Further examination of the waveforms show that, spread through time, the counts change.

Thus the Sigma Delta converter, changes what would otherwise be a full scale amplitude duty cycle at a low frequency, to a variable duty cycle at a much higher frequency that still averages to the same value. This higher frequency variable duty cycle might well have a lower frequency component due to the repetitive count modifications, at the frequency that would be expected for an exact count, but this component is much reduced in spectral amplitude. It is only a modulation, not a fundamental frequency.

A more detailed account of exactly what "noise shaping" is, is described in Noise Shaping As Error Correction.

Summary

It has been shown that the standard amplitude based linear model of Delta-Sigma converters is trivially invalid, and that a model based on duty cycle is mathematically consistent and correctly accounts for characteristics amenable to linear analysis where the standard model fails. Indeed, the standard linear model’s alleged account of noise filtering is entirely delusionary and essentially, explains nothing. The non linear comparator ensures that an amplitude based transfer function argument is DOA.

The Delta-Sigma converter is now seen to be based on an average duty cycle linear transfer function such that feedback is then able to correct for duty cycle errors. It is the large duty cycle gain at low frequencies that allows for the errors to be reduced, not amplitude gain. A Delta Sigma converter, essentially, operates in the time domain, not amplitude domain.

References

1 - “Understanding Sigma-Delta Modulation: The Solved and Unresolved Issues” – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ Joshua D. Reiss, J. Audio Eng. Soc Vol 56 no. ½ MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=1laaaa@384B@ , 2008 January/February

2 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ “An Overview of Sigma-Delta Converters: How a 1-Bit ADC achieves more than 16 bit Resolution” – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ Pervez M. Aziz, Bell Laboratories, Henrik V. Sorensen, Arial Corporation, Jan Van der Spiegel, University of Pennsylvania

3 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ “Delta-Sigma Data Converters, Theory, Design and Simulation” - Norsworthy et al (1997), p143

4 - "Idle tone behaviour in Sigma Delta Modulation" - Enrique Perez Gonzalez1, and Joshua Reiss1, Audio Engineering Society 122nd Convention 2007 May 5 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ 8 Vienna, Austria

5 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ “Sigma-Delta Modulators: Tutorial Overview, Design Guide, and State-of-the-Art Survey Circuits and Systems I:” Regular Papers, IEEE Transactions on (Volume:58 , Issue: 1 ) Pub. Dec. 2010

6 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ “ADC Architectures III: Sigma-Delta ADC Basics” - Walt Kester – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ Analog Devise App note MT-022

7 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ “ADC Architectures IV: Sigma-Delta ADC Advanced Concepts and Applications" - Walt Kester - Analog Devices App note MT-023

8 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ “Demystifying Delta-Sigma ADCs” Tutorial 1870 - App Note – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ Jan 31, 2003 - Maxim Integrated

9 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ “How delta-sigma ADCs work, Part 1” - Bonnie Baker - App Note - Texas Instruments

10 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ “Principals of Sigma Delta Modulation for Analog to Digital Converters” - Sangil Park, Ph. D. – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ Motorola

11 "Delta Sigma AD Conversion Technique Overview" - AN10 -Crystal Semiconductor, A Cirrus Logic Company.

“…The quantization noise at the output is reduced by the open-loop gain of the integrator. At low frequency, the integrator is designed for high open-loop gain, so that quantization noise is reduced...”

12 "Why 1-Bit Sigma-Delta Conversion is Unsuitable for High-Quality Applications" - Stanley P. Lipshitz and John Vanderkooy Audio Research Group, University of Waterloo

Waterloo, Ontario N2L 3G1, Canada - Audio Engineering Society Convention Paper 5395 Presented at the 110th Convention 2001 May 12 – MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbyaqaaaaaaaaaWdbiaa=nbiaaa@37C1@ 15 Amsterdam, The Netherlands

23 - Noise Shaping As Error Correction

The information on the page may be reproduced

providing that this source is acknowledged.

Website last modified 30^th August 2013