The Twins Paradox
A Correct
Analysis
Kevin
Aylward B.Sc.
kevin@kevinaylward.co.uk
22/11/2025
Origin ~
2013
Abstract
The
“Twins Paradox” is the notion that, if both observers, in different reference
frames, view the other observer as exhibiting time dilation, how is it that one
twin ages less than the other when one twin undergoes a round trip to a distant
star and back?
The
presentation here explains how the paradox is resolved, and does so without any
requirement to explain the asymmetry either by the acceleration that one twin
experiences, or because that twin switches their frame of reference on return.
Overview
The
twins paradox is the notion that if the Principle of Relativity (POR) is valid,
then if one twin jaunts off in a rocket to the star Alpha Centauri at a speed
close to the velocity of light and returns, it is concluded that there is
ambiguity in what twin shows the least age. The argument being that Special
Relativity (SR) states that the observed clock ticks of a clock in a frame
moving relatively to a clock in a notional stationary frame, are larger, such
that time (number of clock ticks) for the moving clock passes slower than the
non-moving clock. However, it is also
stated that the traveller can consider himself fixed in space, such that the
stay at home twin may be considered to be moving such that the stay at home
twin can claim to be the younger twin.
There
are many accounts of claims of resolving the twins paradox of Special Relativity
such as whether acceleration is required, for example trips through
“space-time” and some claiming that it is due to switching the direction of frames
for the traveller that the stay at home does not experience.
These
explanations are not correct. Fundamentally, they have lost the plot.
Neither
frame switching or acceleration form the root cause as to why the
traveller is younger.
The root cause is that the stay at home twin and the star are both in a different frame from the travelling twin.
The frames are different because the star always stays in the same frame as the
stay at home twin, whatever frame is taken to be at rest. The times in different frames are different because time
in frames is dependent on distance as well as time of other frames.
This is absolutely fundamental to the resolution of the paradox. This changes
the distances that the traveller measures from that which the stay at home twin
measures. The fact that frame times depend on distance is typically ignored.
Thus
the root cause of the asymmetry in times of the twins is:
1 The stay at home twin measures event
times at two different locations.
That is, the stay at home twin and the star do not
move with respect to each other, but the traveller twin moves with respect to both
the stay at home twin and the star.
2 The traveller, considered at rest,
measures event times at one location.
That is, the traveller is considered at rest with
respect to both the stay at home twin and the star, but the stay at home twin
and the star both move with respect to the traveller.
Whether
or not there is a paradox, is whether or not a correct application of the Lorentz Transform results in the same
results for the time of the trip, independent of who is considered at rest.
Hand waving descriptions typically ignore what the true physics actually says.
Typically most alleged resolutions don’t actually show the calculations of both
viewpoints, they engage in a Strawman that notionally appears to do this, but
doesn’t.
Indeed,
whether the moving clock is outward or inward makes no difference. According to
a correct
SR calculation, both twins will agree as to the time difference between the start event
and end events of even the single way trip, and that the traveller is the
youngest, eliminating the paradox.
However…
There
is an obvious corollary to the recognition that that the asymmetry in the twins,
is that the stay at home twin and the star must always be always be considered
to move together. That is, the usual argument ignores that there must be two
locations that must be considered moving, not just the stay at home twin moving.
The
corollary is that the usual argument of taking two objects and noting that any one
on its own can be considered as the mover, is flawed.
The
rest of the universe actually exists.
To
ensure that the relativity postulate is correctly applied, the entire
universe must be considered moving, when the notionally moving system is now
considered to be stationary.
That
is, object A notionally at rest, interacts with all other objects subject to
that specific condition. Object B moves with respect to all other objects in the
universe.
So,
there is a fundamental asymmetry when applying the relativity postulate correctly,
usually ignored.
The
stay at home twin never moves with respect to the rest of the universe when
considered at rest or moving, but the traveller twin must always be considered
moving with respect to the universe.
Noting
the claim of this objective fact, is certain to raise the eyebrows from those
that just haven’t thought about the problem in enough depth.
There
is an asymmetry as to who is moving with respect to the universe.
Calculation
However,
whether one has any reservations as to the relevance of relative motion to the
universe, such a notion is immaterial to correctly calculating from the Lorentz
Transform the asymmetry of the twins elapsed times, agreed upon by both twins.
The
key point is:
1
Time in a frame is not simply:
t
'
=γt
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDamaaCaaaleqabaGaai4jaaaakiabg2da9iabeo7aNjaadshaaaa@3B56@
- 1
It
is:
t
'
=γ(t−
vx
c
2
)
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDamaaCaaaleqabaGaai4jaaaakiabg2da9iabeo7aNjaacIcacaWG0bGaeyOeI0YaaSaaaeaacaWG2bGaamiEaaqaaiaadogadaahaaWcbeqaaiaaikdaaaaaaOGaaiykaaaa@4180@
- 2
That
is, time events in inertial frames are dependent on both time events in the frames and
distance travelled in that frame.
2
Distances (lengths) in frames are not
the same, they are related by:
x
'
=γx
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCaaaleqabaGaai4jaaaakiabg2da9iabeo7aNjaadIhaaaa@3B5E@
- 3
The System
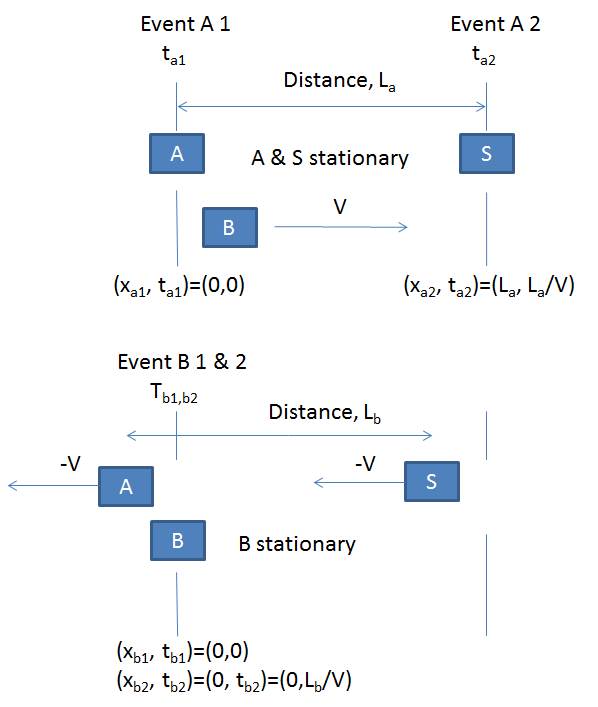
Diagram 1 Traveller Model
A
= Stay at home twin
B
= Travelling twin
S
= Star
La
= Rest frame distance of stay at home twin to the star, as measured by the stay
at home twin
Lb
= Rest frame distance of traveller twin measured for distance of stay at home
twin to the star
Event
1 = Time & space coordinates of
when B and A are at the same location
Event
2 = Time & space coordinates of
when B and S are at the same location
The
coordinates should be clear from simple inspection. It takes a time of L/V to
get to the star. The time coordinate for the case where B is considered
stationary is simply B’s own clock time.
The Calculations
The
Lorentz Transform (LT) allows the time
and space coordinates of events in one frame to be calculated from time and space coordinates of events in
another frame. That is:
x
'
=γ(x−vt)
t
'
=γ(t−
vx
c
2
)
γ=
1
1−
v
2
c
2
1
γ
2
=(1−
v
2
c
2
)
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWG4bWaaWbaaSqabeaacaGGNaaaaOGaeyypa0Jaeq4SdCMaaiikaiaadIhacqGHsislcaWG2bGaamiDaiaacMcaaeaacaWG0bWaaWbaaSqabeaacaGGNaaaaOGaeyypa0Jaeq4SdCMaaiikaiaadshacqGHsisldaWcaaqaaiaadAhacaWG4baabaGaam4yamaaCaaaleqabaGaaGOmaaaaaaGccaGGPaaabaGaeq4SdCMaeyypa0ZaaSaaaeaacaaIXaaabaWaaOaaaeaacaaIXaGaeyOeI0YaaSaaaeaacaWG2bWaaWbaaSqabeaacaaIYaaaaaGcbaGaam4yamaaCaaaleqabaGaaGOmaaaaaaaabeaaaaaakeaadaWcaaqaaiaaigdaaeaacqaHZoWzdaahaaWcbeqaaiaaikdaaaaaaOGaeyypa0JaaiikaiaaigdacqGHsisldaWcaaqaaiaadAhadaahaaWcbeqaaiaaikdaaaaakeaacaWGJbWaaWbaaSqabeaacaaIYaaaaaaakiaacMcaaaaa@5F9A@
- 4
Thus,
given the coordinates of events 1 & 2 according to A, then the coordinates
of B for events 1 & 2 can be calculated as:
x
b1
=γ(
x
a1
−v
t
a1
)
t
b1
=γ(
t
a1
−
v
x
a1
c
2
)
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWG4bWaaSbaaSqaaiaadkgacaaIXaaabeaakiabg2da9iabeo7aNjaacIcacaWG4bWaaSbaaSqaaiaadggacaaIXaaabeaakiabgkHiTiaadAhacaWG0bWaaSbaaSqaaiaadggacaaIXaaabeaakiaacMcaaeaacaWG0bWaaSbaaSqaaiaadkgacaaIXaaabeaakiabg2da9iabeo7aNjaacIcacaWG0bWaaSbaaSqaaiaadggacaaIXaaabeaakiabgkHiTmaalaaabaGaamODaiaadIhadaWgaaWcbaGaamyyaiaaigdaaeqaaaGcbaGaam4yamaaCaaaleqabaGaaGOmaaaaaaGccaGGPaaaaaa@5492@
- 5
x
b2
=γ(
x
a2
−v
t
a2
)
t
b2
=γ(
t
a2
−
v
x
a2
c
2
)
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWG4bWaaSbaaSqaaiaadkgacaaIYaaabeaakiabg2da9iabeo7aNjaacIcacaWG4bWaaSbaaSqaaiaadggacaaIYaaabeaakiabgkHiTiaadAhacaWG0bWaaSbaaSqaaiaadggacaaIYaaabeaakiaacMcaaeaacaWG0bWaaSbaaSqaaiaadkgacaaIYaaabeaakiabg2da9iabeo7aNjaacIcacaWG0bWaaSbaaSqaaiaadggacaaIYaaabeaakiabgkHiTmaalaaabaGaamODaiaadIhadaWgaaWcbaGaamyyaiaaikdaaeqaaaGcbaGaam4yamaaCaaaleqabaGaaGOmaaaaaaGccaGGPaaaaaa@5498@
- 6
The Usually Included Calculation
For
diagram 1, the time A calculates for the trip from event 1 to 2, is event 2
time
–
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbCaqaaaaaaaaaWdbiaa=nbiaaa@3801@
event 1 time
is:
t
a12
=
t
a2
−
t
a1
=(
L
a
v
−0)=
L
a
v
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDamaaBaaaleaacaWGHbGaaGymaiaaikdaaeqaaOGaeyypa0JaamiDamaaBaaaleaacaWGHbGaaGOmaaqabaGccqGHsislcaWG0bWaaSbaaSqaaiaadggacaaIXaaabeaakiabg2da9iaacIcadaWcaaqaaiaadYeadaWgaaWcbaGaamyyaaqabaaakeaacaWG2baaaiabgkHiTiaaicdacaGGPaGaeyypa0ZaaSaaaeaacaWGmbWaaSbaaSqaaiaadggaaeqaaaGcbaGaamODaaaaaaa@4BF1@
- 7
Also
from diagram 1
(
x
a1
,
t
a1
)=(0,0)
(
x
a2
,
t
a2
)=(
L
a
,
L
a
v
)
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaGGOaGaamiEamaaBaaaleaacaWGHbGaaGymaaqabaGccaGGSaGaamiDamaaBaaaleaacaWGHbGaaGymaaqabaGccaGGPaGaeyypa0JaaiikaiaaicdacaGGSaGaaGimaiaacMcaaeaacaGGOaGaamiEamaaBaaaleaacaWGHbGaaGOmaaqabaGccaGGSaGaamiDamaaBaaaleaacaWGHbGaaGOmaaqabaGccaGGPaGaeyypa0JaaiikaiaadYeadaWgaaWcbaGaamyyaaqabaGccaGGSaWaaSaaaeaacaWGmbWaaSbaaSqaaiaadggaaeqaaaGcbaGaamODaaaacaGGPaaaaaa@51AF@
- 8
Thus
the coordinates of B for event 1 are:
(
x
b1
,
t
b1
)=γ(0−v×0,0−
v×
0
c
2
)=(0,0)
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadIhadaWgaaWcbaGaamOyaiaaigdaaeqaaOGaaiilaiaadshadaWgaaWcbaGaamOyaiaaigdaaeqaaOGaaiykaiabg2da9iabeo7aNjaacIcacaaIWaGaeyOeI0IaamODaiabgEna0kaaicdacaGGSaGaaGimaiabgkHiTmaalaaabaGaamODaiabgEna0kaaicdadaWgaaWcbaaabeaaaOqaaiaadogadaahaaWcbeqaaiaaikdaaaaaaOGaaiykaiabg2da9iaacIcacaaIWaGaaiilaiaaicdacaGGPaaaaa@53C4@
- 9
The
coordinates of B for event 2 are:
(
x
b2
,
t
b2
)=γ(
L
a
−v×
L
a
v
,
L
a
v
−
v×
L
a
c
2
)=γ(0,
L
a
v
(1−
v
2
c
2
))=(0,
L
a
γv
)
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadIhadaWgaaWcbaGaamOyaiaaikdaaeqaaOGaaiilaiaadshadaWgaaWcbaGaamOyaiaaikdaaeqaaOGaaiykaiabg2da9iabeo7aNjaacIcacaWGmbWaaSbaaSqaaiaadggaaeqaaOGaeyOeI0IaamODaiabgEna0oaalaaabaGaamitamaaBaaaleaacaWGHbaabeaaaOqaaiaadAhaaaGaaiilamaalaaabaGaamitamaaBaaaleaacaWGHbaabeaaaOqaaiaadAhaaaGaeyOeI0YaaSaaaeaacaWG2bGaey41aqRaamitamaaBaaaleaacaWGHbaabeaakmaaBaaaleaaaeqaaaGcbaGaam4yamaaCaaaleqabaGaaGOmaaaaaaGccaGGPaGaeyypa0Jaeq4SdCMaaiikaiaaicdacaGGSaWaaSaaaeaacaWGmbWaaSbaaSqaaiaadggaaeqaaaGcbaGaamODaaaacaGGOaGaaGymaiabgkHiTmaalaaabaGaamODamaaCaaaleqabaGaaGOmaaaaaOqaaiaadogadaahaaWcbeqaaiaaikdaaaaaaOGaaiykaiaacMcacqGH9aqpcaGGOaGaaGimaiaacYcadaWcaaqaaiaadYeadaWgaaWcbaGaamyyaaqabaaakeaacqaHZoWzcaWG2baaaiaacMcaaaa@6DCF@
- 10
Thus
A concludes that the time B calculates for the trip from event 1 to 2, is event
2 time
–
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaacbaqcLbCaqaaaaaaaaaWdbiaa=nbiaaa@3801@
event 1 time
is:
t
b21
=
t
b2
−
t
b1
=(
L
a
γv
−0)=
L
a
γv
=
t
a21
γ
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDamaaBaaaleaacaWGIbGaaGOmaiaaigdaaeqaaOGaeyypa0JaamiDamaaBaaaleaacaWGIbGaaGOmaaqabaGccqGHsislcaWG0bWaaSbaaSqaaiaadkgacaaIXaaabeaakiabg2da9iaacIcadaWcaaqaaiaadYeadaWgaaWcbaGaamyyaaqabaaakeaacqaHZoWzcaWG2baaaiabgkHiTiaaicdacaGGPaGaeyypa0ZaaSaaaeaacaWGmbWaaSbaaSqaaiaadggaaeqaaaGcbaGaeq4SdCMaamODaaaacqGH9aqpdaWcaaqaaiaadshadaWgaaWcbaGaamyyaiaaikdacaaIXaaabeaaaOqaaiabeo7aNbaaaaa@558B@
- 11
That
is:
t
b21
=
t
a21
γ
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDamaaBaaaleaacaWGIbGaaGOmaiaaigdaaeqaaOGaeyypa0ZaaSaaaeaacaWG0bWaaSbaaSqaaiaadggacaaIYaGaaGymaaqabaaakeaacqaHZoWzaaaaaa@3FAB@
-
12
The Usually Ignored Calculation
Now…
the bit that is pretty much always missed missed…what does B actually calculate for the time A experiences between event
1 and event 2, not what is ad-hoc claimed?
To
do this, one needs to calculate A’s coordinates, given B’s coordinates, that
is:
x
a1
=γ(
x
b1
+v
t
b1
)
t
a1
=γ(
t
b1
+
v
x
b1
c
2
)
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWG4bWaaSbaaSqaaiaadggacaaIXaaabeaakiabg2da9iabeo7aNjaacIcacaWG4bWaaSbaaSqaaiaadkgacaaIXaaabeaakiabgUcaRiaadAhacaWG0bWaaSbaaSqaaiaadkgacaaIXaaabeaakiaacMcaaeaacaWG0bWaaSbaaSqaaiaadggacaaIXaaabeaakiabg2da9iabeo7aNjaacIcacaWG0bWaaSbaaSqaaiaadkgacaaIXaaabeaakiabgUcaRmaalaaabaGaamODaiaadIhadaWgaaWcbaGaamOyaiaaigdaaeqaaaGcbaGaam4yamaaCaaaleqabaGaaGOmaaaaaaGccaGGPaaaaaa@547E@
- 13
Noting
the change in the direction of the motion as viewed by B.
The
coordinates of B, from the diagram are:
(
x
b1
,
t
b1
)=(0,0)
(
x
b2
,
t
b2
)=(0,
t
b2
)
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaGGOaGaamiEamaaBaaaleaacaWGIbGaaGymaaqabaGccaGGSaGaamiDamaaBaaaleaacaWGIbGaaGymaaqabaGccaGGPaGaeyypa0JaaiikaiaaicdacaGGSaGaaGimaiaacMcaaeaacaGGOaGaamiEamaaBaaaleaacaWGIbGaaGOmaaqabaGccaGGSaGaamiDamaaBaaaleaacaWGIbGaaGOmaaqabaGccaGGPaGaeyypa0JaaiikaiaaicdacaGGSaGaamiDamaaBaaaleaacaWGIbGaaGOmaaqabaGccaGGPaaaaaa@505A@
- 14
Thus
the coordinates of A for event 1 are:
(
x
a1
,
t
a1
)=γ(0+v×0,0+
v×
0
c
2
)=(0,0)
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadIhadaWgaaWcbaGaamyyaiaaigdaaeqaaOGaaiilaiaadshadaWgaaWcbaGaamyyaiaaigdaaeqaaOGaaiykaiabg2da9iabeo7aNjaacIcacaaIWaGaey4kaSIaamODaiabgEna0kaaicdacaGGSaGaaGimaiabgUcaRmaalaaabaGaamODaiabgEna0kaaicdadaWgaaWcbaaabeaaaOqaaiaadogadaahaaWcbeqaaiaaikdaaaaaaOGaaiykaiabg2da9iaacIcacaaIWaGaaiilaiaaicdacaGGPaaaaa@53AC@
- 15
The
coordinates of A for event 2 are:
(
x
a2
,
t
a2
)=γ(0+v×
t
b2
,
t
b2
+0)=γ(
L
b
,
t
b2
)
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadIhadaWgaaWcbaGaamyyaiaaikdaaeqaaOGaaiilaiaadshadaWgaaWcbaGaamyyaiaaikdaaeqaaOGaaiykaiabg2da9iabeo7aNjaacIcacaaIWaGaey4kaSIaamODaiabgEna0kaadshadaWgaaWcbaGaamOyaiaaikdaaeqaaOGaaiilaiaadshadaWgaaWcbaGaamOyaiaaikdaaeqaaOGaey4kaSIaaGimaiaacMcacqGH9aqpcqaHZoWzcaGGOaGaamitamaaBaaaleaacaWGIbaabeaakiaacYcacaWG0bWaaSbaaSqaaiaadkgacaaIYaaabeaakiaacMcaaaa@579E@
- 16
Thus
B concludes that A’s distance to the star, and its time difference between
events is:
(
x
a21
,
t
a21
)=γ(
L
b
,
t
b2
)−(0,0)=γ(
L
b
,
t
b2
)
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadIhadaWgaaWcbaGaamyyaiaaikdacaaIXaaabeaakiaacYcacaWG0bWaaSbaaSqaaiaadggacaaIYaGaaGymaaqabaGccaGGPaGaeyypa0Jaeq4SdCMaaiikaiaadYeadaWgaaWcbaGaamOyaaqabaGccaGGSaGaamiDamaaBaaaleaacaWGIbGaaGOmaaqabaGccaGGPaGaeyOeI0IaaiikaiaaicdacaGGSaGaaGimaiaacMcacqGH9aqpcqaHZoWzcaGGOaGaamitamaaBaaaleaacaWGIbaabeaakiaacYcacaWG0bWaaSbaaSqaaiaadkgacaaIYaaabeaakiaacMcaaaa@5650@
- 17
That
is, B concludes that A’s length and time is:
x
a21
=γ
L
b
t
a21
=γ
t
b21
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWG4bWaaSbaaSqaaiaadggacaaIYaGaaGymaaqabaGccqGH9aqpcqaHZoWzcaWGmbWaaSbaaSqaaiaadkgaaeqaaaGcbaGaamiDamaaBaaaleaacaWGHbGaaGOmaiaaigdaaeqaaOGaeyypa0Jaeq4SdCMaamiDamaaBaaaleaacaWGIbGaaGOmaiaaigdaaeqaaaaaaa@47C3@
- 18
That
is, B concludes, by simple algebra, that:
L
b
=
x
a21
γ
=
L
a
γ
t
b21
=
t
a21
γ
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGGipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGmbWaaSbaaSqaaiaadkgaaeqaaOGaeyypa0ZaaSaaaeaacaWG4bWaaSbaaSqaaiaadggacaaIYaGaaGymaaqabaaakeaacqaHZoWzaaGaeyypa0ZaaSaaaeaacaWGmbWaaSbaaSqaaiaadggaaeqaaaGcbaGaeq4SdCgaaaqaaiaadshadaWgaaWcbaGaamOyaiaaikdacaaIXaaabeaakiabg2da9maalaaabaGaamiDamaaBaaaleaacaWGHbGaaGOmaiaaigdaaeqaaaGcbaGaeq4SdCgaaaaaaa@4C97@
- 19
Thus
the time that B concludes A measures for B’s events, is exactly the same as
that A (eq. 12) concludes B measures for B’s events, both agree that B reads
less time, thus there is no
paradox.
That
is, both A & B conclude that making a one way trip to the star results in
less time for B. Returning just
results in doubling up the time, as can be easily calculated simply by resetting
t=0 at the star and performing, the same calculation with velocities swapped.
The
crucial point is that B views the distance from A to the star as shorter, thus
B views events that are synchronised by that length, take less time. Thus
despite a notional symmetrical γ in the transform equations when inverting
viewpoints, γ is not the sole determinator of the time between events.
The Simplified Solution Without Time Dilation!
Somewhat
ironically, the Twins Paradox is resolvable without the explicit inclusion of
time dilation at all. One only has to consider the situation from the point of
how the Earth Twin, Traveller Twin and Star are perceived from the point of
length contraction.
The
distance the Earth Twin determines for the distance from the Earth to the Star,
is the distance in the rest frame of the Earth Twin and Star:
This
distance is always the same for the Earth Twin, independent as to whether the
Earth twin, including the Star, is considered at rest or moving. This is
because for both conditions, the Earth and Star are in the same frame, whether considered
at rest or moving together.
Thus
the time the Earth Twin measures for the time the traveller takes from getting
from the Earth to the Star is:
T1
= L/v
The
distance the Earth Twin determines for the distance from the Earth to the Star
for the Traveller Twin is not the same as the Earth Twin as the Traveller Twin
is in a different frame. This distance is given by the Lorentz contraction
factor 1/g. Thus the time the Earth Twin concludes the time occurring for the
Traveller Twin as:
T2
= L/vg
The
Traveller Twin is in a different frame than the Earth & Star frame, so the
Traveller twin, considered travelling, also considers that the distance from
the Earth to the Star is Lorentz contracted, thus incurring a time of travel
as:
T3=
L/vg
The
Traveller Twin, considered at rest, views the Earth and Star go by the
Traveller Twin at a velocity, thus is Lorentz contracted and concludes a time
between the Earth and Star passing as:
T4
= L/vg
The
distance the Traveller Twin determines for the distance from the Earth to the
Star as determined by the Earth Twin, is not Lorentz contracted and thus
concludes the time for the Earth Twin for the time between the Earth and Star
as:
T5
= L/v
The
summary is:
Both
Twins considers the time it takes to go from the Earth to the Star for the
Earth Twin is based on the time of the normal length L.
Both
Twins considers the time it takes to go from the Earth to the Star for the
Traveller Twin is based on the contracted length L/g
It’s
the difference in effective lengths that are asymmetrical, because the Star and
Earth are in one frame, and the Traveller is in another frame. It’s the time to
transverse the lengths that matter, not time dilation.
The
complication in the explanation is that SR holds that lengths are not
physically shortened but are rotated in time, which leads into other issues….
Epilogue
The
Twins Paradox is resolvable without acceleration or frame switching.
This
analysis highlights that it is not correct to only consider that it is either A
or B that can be considered moving, according to the relativity postulate.
A
correct application of the relativity postulate requires, as a minimum, a third
object C, such that the A and C are always locked together. Without a third
object it is impossible to deal with the length aspect of the Lorentz Transform.
The
recognition of the requirement for a third object introduces the elephant in
the room, almost always ignored. That is, object C can only logically be, the
entire universe. Unless the entire universe is considered moving, switching who
is moving cannot be an equivalent system.
It
should be noted that the Lorentz Transform is only a mathematical, behavioural,
calculation machine. It provides no argument as to how or why it accounts for
observations.
